# Parallel processing for computing signed distance functions

SignedDistanceFunction.jl - github (opens new window)

# TL;DR

SignedDistanceFunction.jl was the subject of my senior thesis.

The subject is "Parallel processing for computing signed distance functions", but I actually did a little more than that: in addition to speeding up the parallelization, I also worked on the phase changes in the signing.

As a result, I was able to speed up the calculations while meeting the requirements.

benchmarks

Fig 1. (a) isinside() with the jordan curve / (b) Thinning-Flood fill with the jordan curve / (c) Thinning-Flood fill with multiple curves

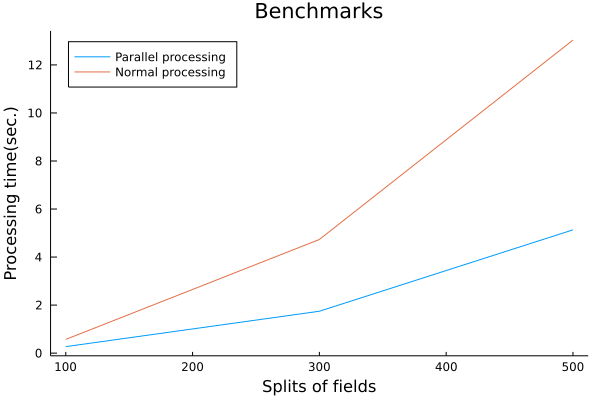
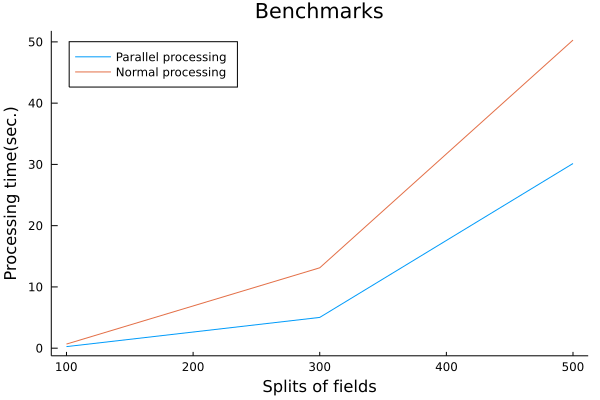
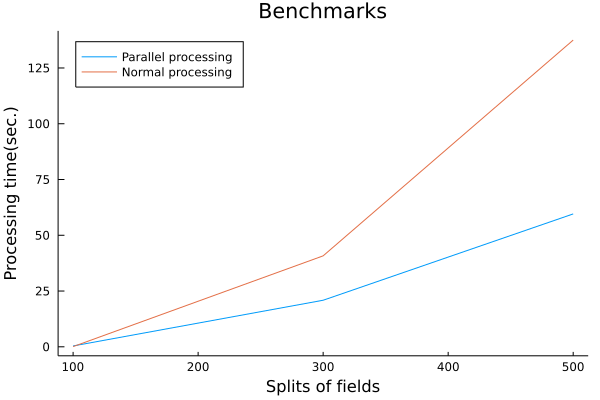
# What are "signed distance functions" for?

The Level Set method is known as the way of tracking interfaces in the subdomain. The snakes method is also known like as that, but the Level Set method is better because it is able to deal with phase changes.

The Level Set method considers the region of interest to be the zero contour surface of a first-dimensional higher-order surface in the region, and is represented by a first-order partial differential equation. Therefore, one initial condition is required.

The signed distance function is often used as the initial value of the level set method. The purpose of this research is to create something that will improve the speed of this calculation, since it is very heavy.

# What is the "SignedDistanceFunction"?

The signed distance function is simply a function that returns the distance from any point in a region to a closed curve in that region, where the distance is returned as a negative (or positive) number if inside the closed curve, and given as the opposite if outside.

The closed curve is given by discrete as images below and subdomains also will be discrete model. The distance is calculated from Each points in subdomains to every closed curve point as images below. The shortest distance of that result will be the element of points in the subdomain that represented by matrix.

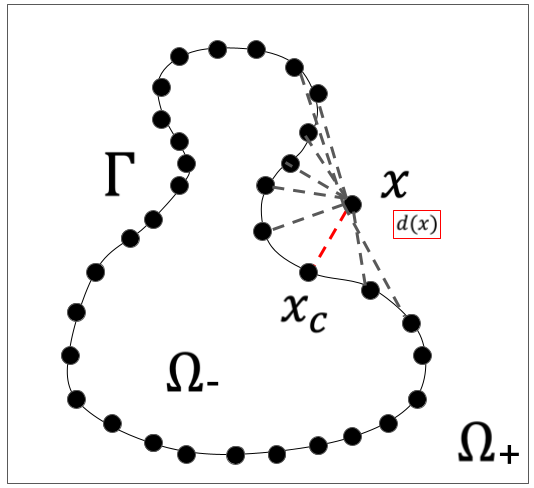
Fig 2. calculates distance from any point to closed curve in a region.

For example, if the inside is set to be negative, the result is expected as below.

Fig 3.

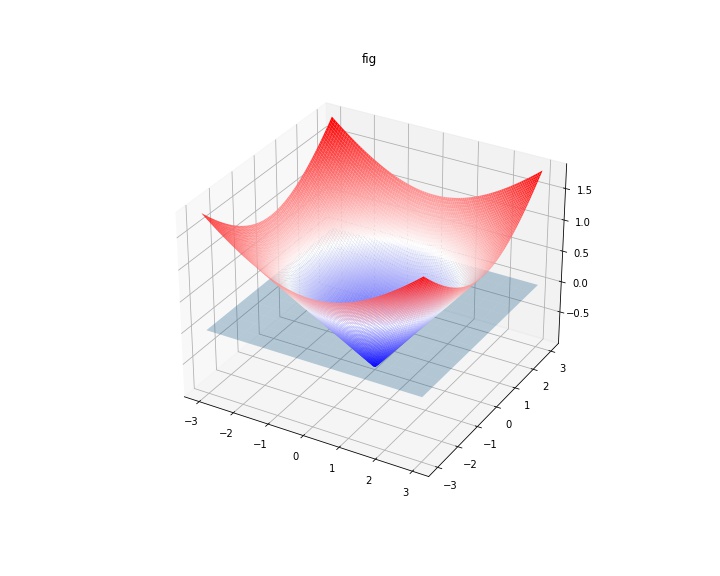
# On a simple case

First, When starting out, the initial research objective was the "computing signed distance functions in parallel".

Under that objective, the requirements were clear. All I had to do was to parallelize the generation of the distance functions and benchmark them to see how much faster the process was.

The parallelization of the distance function generation was very easy to implement in the Julia language because the calculations of the distance function generation are independent of each other and can be easily parallelized by Julia's Threads.@threads macro.

The signing was also easy to do using Luxor.jl's isinside(). The result is the following Plot.

Fig 4.

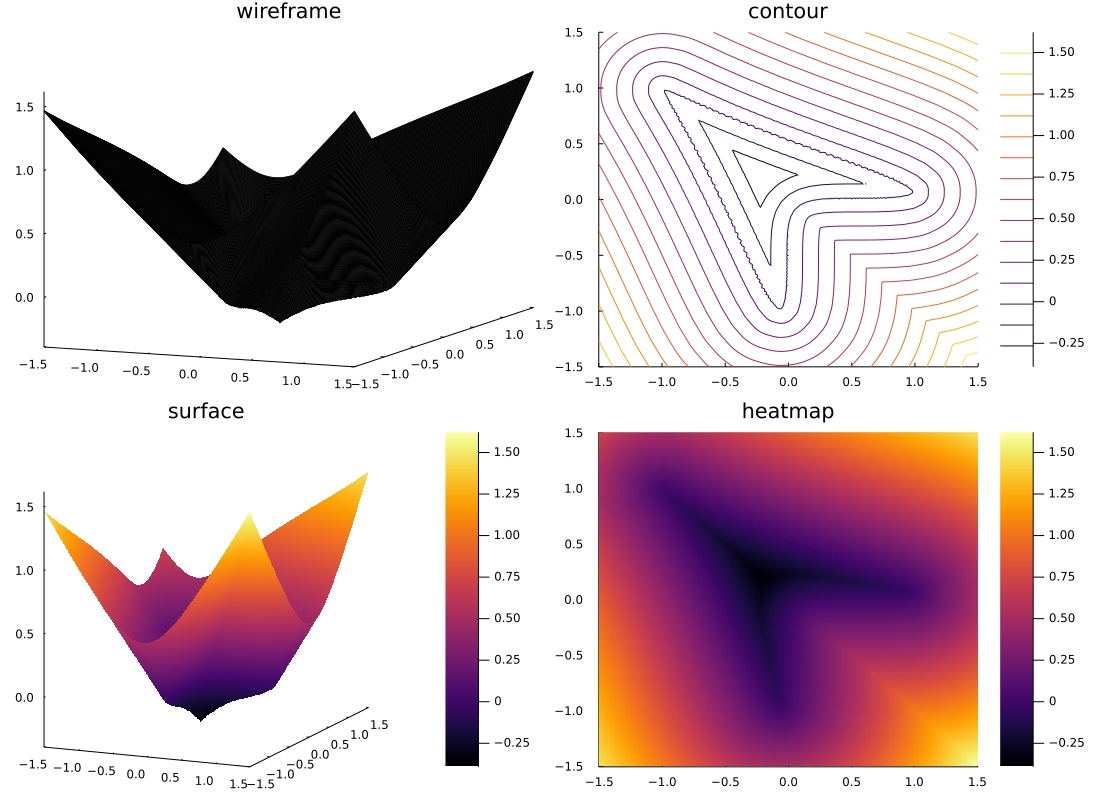
# On a complicated cases

However, when multiple closed curves exist in a subdomain, isinside() could not be used. Therefore, another method for signing had to be considered. Though there are multiple regions that must be recognized as the inside of a closed curve, there is only one region that is recognized as the exterior. Focusing on this, we used the famous FloodFiil algorithm for coloring. To be precise, I used a slightly modified version of it called Thinning-Flood fill. Thinning-Flood fill is a modified algorithm for flood fill that I devised. The procedure is as follows.

1. Apply the usual flood-fill algorithm to the elements of the matrix that represent the discretized subdomain, skipping one element at a time.
1. Next, the points between the encoded elements are encoded according to the following rules(Thinning Rule).
- 2-1. Decide on either the vertical or horizontal direction, and encode half of the unencoded grid points. In this case, we will encode in the vertical direction first.
  - (1) In case of no lines between the the signed grid points.
    - Sign the same symbol as the upper and lower grid points's symbols.
  - (2) In case of being lines between the the signed grid points.
    - If a closed curve exists above an uncoded grid point, give it the same sign as that of the lower grid point.
    - If a closed curve exists lower an uncoded grid point, give it the same sign as that of the upper grid point.

The calculations in (1) and (2) of 2-1. of the Thinning Rule are independent, so they can also be parallelized.

This allowed us to generate a signed distance function as shown below.

Fig 5.

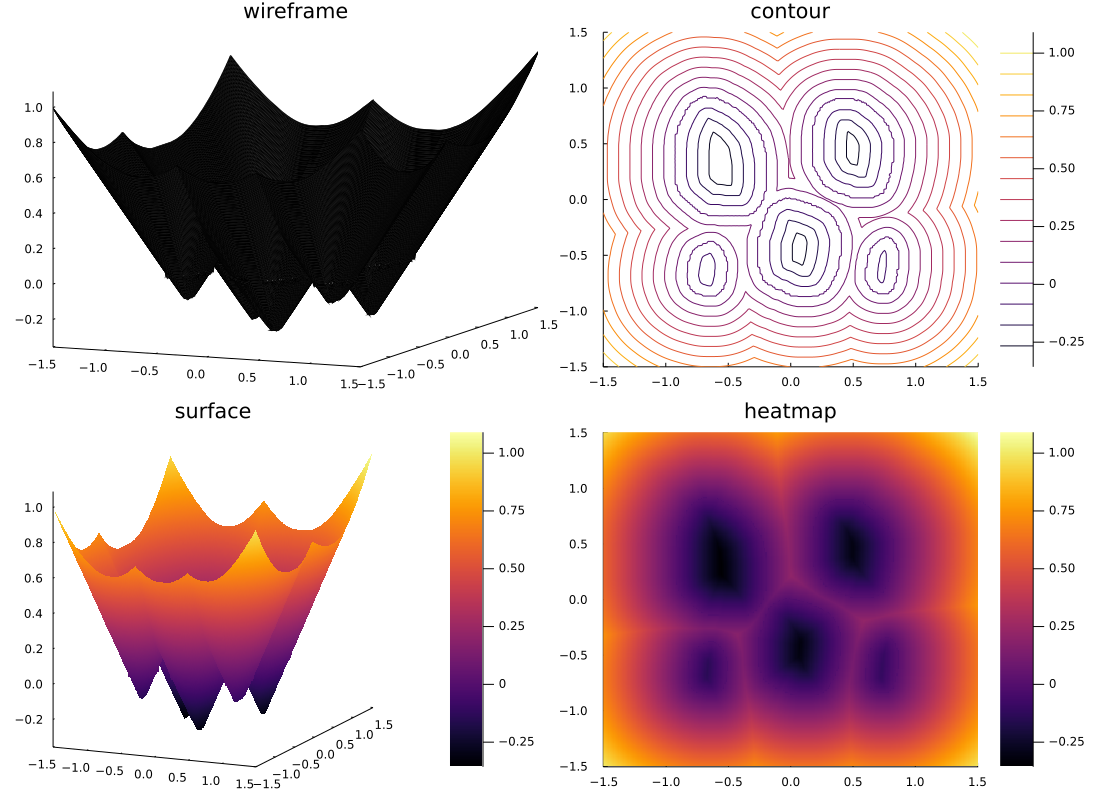
# Development KPT

# Keep

I set Makefile that Run shell script, so the development procedure was like TDD.
As shown in Demo-for-SignedDistanceFunction.jl (opens new window), I implemented a painting board so that I could quickly create data for mock.
In the final stages of development, I set the main branch the master, staging, and release branches, and the release branch the default branch. This will allow us to avoid Makefiles and shell scripts in the release version.

# Problems

Some docstrings are not appropriate or nothing, and some method name is also not good...

# Try

Docstring and method names need to be refactored.
I want to release to the official package registry.

# Conclusion

There are still some issues to be resolved, but I think it's a good thing that I was able to introduce the library in a usable state. The structure is in the form of a general package, and as long as I fix the comments, I think I can send a PR to the official package registry. I am very grateful to my professor for providing me with this problem, and I'd like to thank my fellow members for participating in the discussion. By the way, I haven't decided what to do next at all, so I'll create an issue.