# Parallel processing for computing signed distance functions

SignedDistanceFunction.jl - github (opens new window)

# TL;DR

SignedDistanceFunction.jlは、私の卒業論文のテーマでした。

題は符合付き距離函数の並列化となっていますが、実際にやったことはもう少しあって、並列化による高速化の他に、符号化における位相変化への対応も行いました。

結果的には要件を満たしつつ、計算の高速化に成功しました。

benchmarks

Fig 1. (a) isinside() with the jordan curve / (b) Thinning-Flood fill with the jordan curve / (c) Thinning-Flood fill with multiple curves

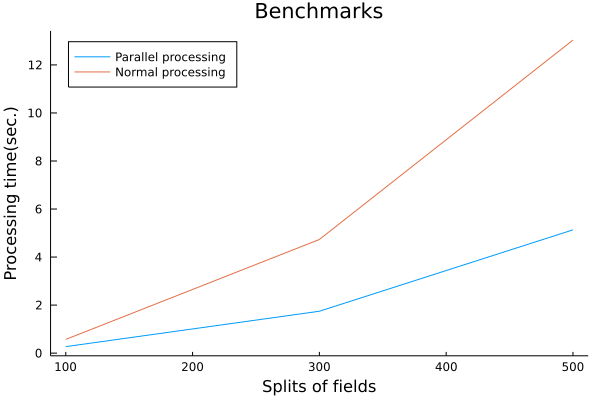
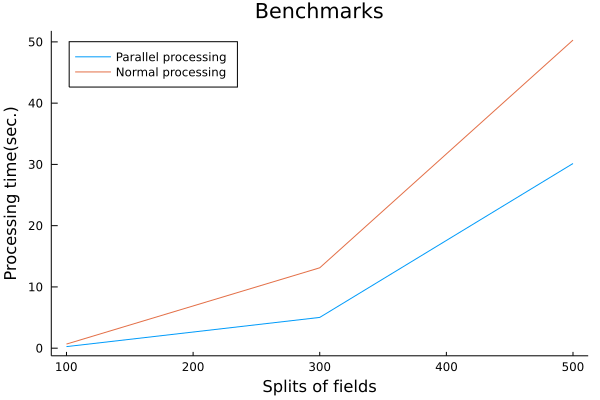
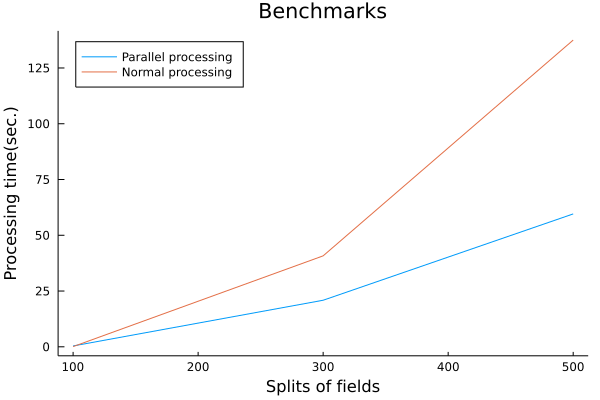
# What are "signed distance functions" for?

サブドメイン内のインターフェイスを追跡する方法として、レベルセット法が知られています。スネーク法もそうですが、相変化に対応できる点で、レベルセット法の方が優れています。

レベルセット法は、対象とする領域をその領域の一次元高次な曲面のゼロ等高面と見なす方法であり、一階偏微分方程式で表現されます。そのため、初期条件が1つ必要です。

往々にしてレベルセット法の初期値として、符合付き距離函数が使われます。これの計算が非常に重いので、この計算の速度を改善する何かを作ろう、というのが研究目的です。

# What is the "SignedDistanceFunction"?

符合付き距離函数というのは、簡潔に言えば、ある領域内にある閉曲線に対する領域内の任意の点からの距離が返ってくる関数のことで、閉曲線の内側であれば距離が負(または正)の数で返され、外側であればその逆として与えられます。

画像のように閉曲線は離散で与えられ、subdomainも離散化します。subdomainの各点において図のように閉曲線の各点への距離を計算します。計算した距離のうち、一番小さい距離をその点からの閉曲線への距離とします。

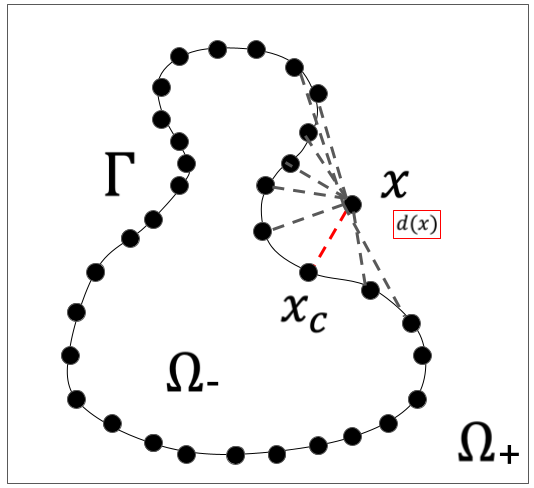
Fig 2. calculates distance from any point to closed curve in a region.

例えば、内側を負にするのであれば、以下のようになることが期待されます。

Fig 3.

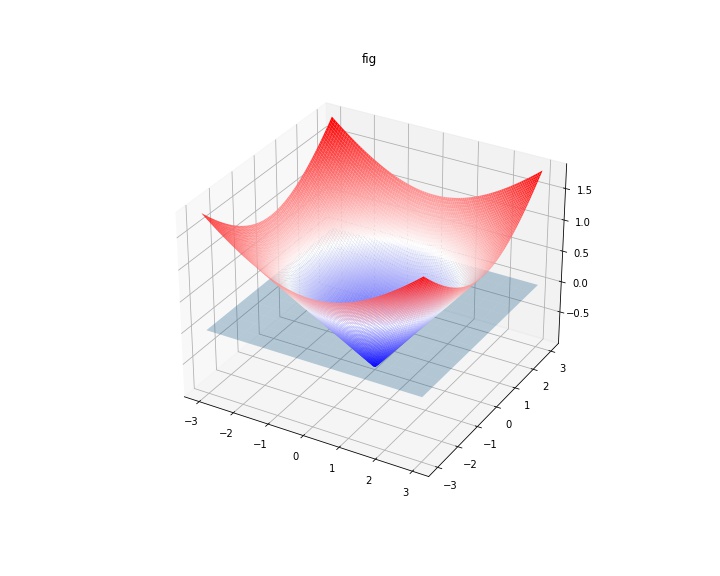
# On a simple case

スタート時の当初の研究目標は「符号付き距離関数を並列に計算する」ことでした。

その目標下であれば、要件はクリアでした。距離函数の生成の並列化をして、ベンチマークをとって、処理どの程度高速化されたかを確かめるのみでした。

距離函数生成の並列化はJulia言語では非常に容易に実装することができました、なぜなら、距離函数の生成の計算はそれぞれ独立しているし、JuliaのThreads.@threadsマクロによって簡単に並列化が行えたからです。

The signing was also easy to do using Luxor.jl's isinside(). The result is the following Plot.

Fig 4.

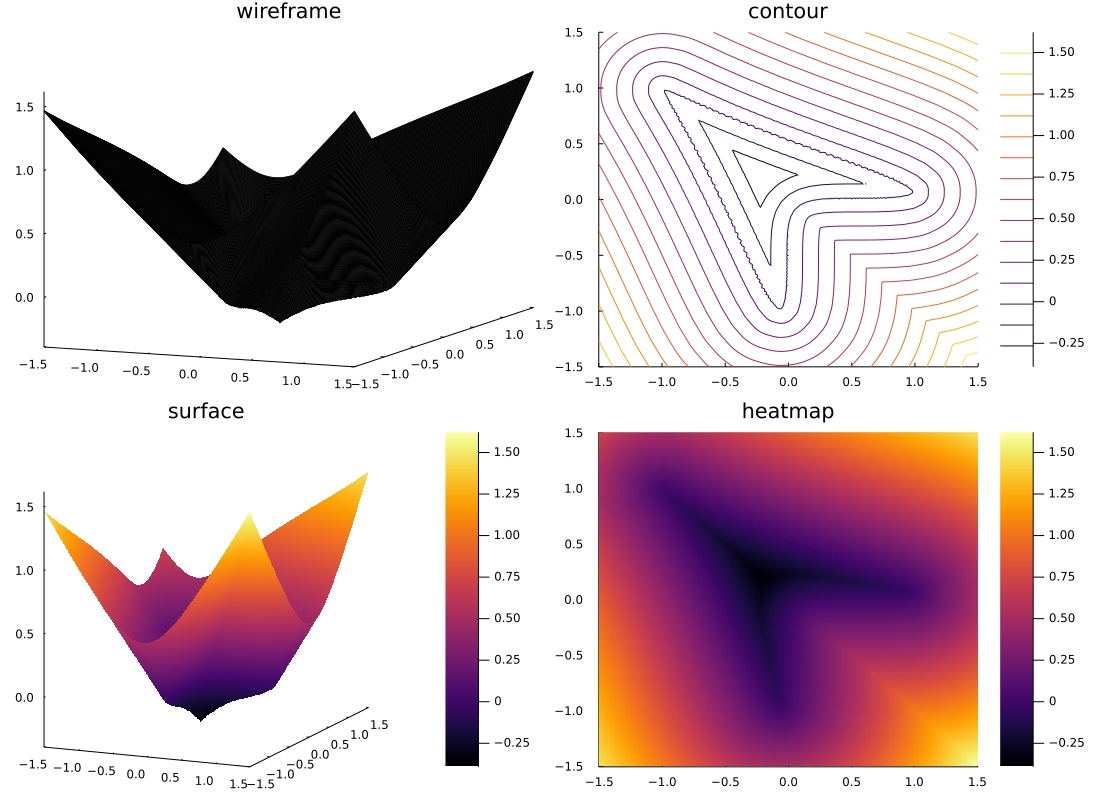
# On a complicated cases

しかし、subdomain内に閉曲線が複数ある場合にはisinside()は使えませんでした。そこで、signingの方法を別で考える必要がありました。閉曲線の内部として認識しなければならない領域は複数ありますが、外部として認識される領域は一つしかありません。これに着目して、色塗りのアルゴリズムとして有名なFloodFiilアルゴリズムを使用しました。正確にはそれを少し変えたThinning-Flood fillという方法を取りました。 Thinning-Flood fillは私が考案したflood fillの修正アルゴリズムです。手順は以下の通りです。

1. 離散化したsubdomainを表したmatrixの要素に対して、一つ飛ばしで通常のFlood-fillアルゴリズムを適用します。
1. 次に、符号化した要素の間にある点の符号化を以下のルール(Thinning Rule)に従って行います
- 2-1. 縦方向か横方向のどちらかの方向を決めて、符号化されていないgrid pointの半分を符号化していく。ここでは最初に縦方向で符号化を進める。
  - (1) 符合化された点と点の間に閉曲線がない場合
    - 符号化された上下の符号と同じ符合を付与する。
  - (2) 間に閉曲線がある場合
    - 符号化されてないgrid pointより上に閉曲線がある場合は、下側のgrid pointの符号と同じ符合を付与する
    - 符号化されてないgrid pointより下に閉曲線がある場合は、上側のgrid pointの符号と同じ符合を付与する

Thinning Ruleの2-1. の(1), (2)の計算は独立しているのでこれも並列化が可能です。

これにより以下のように符合付き距離函数を生成することができました。

Fig 5.

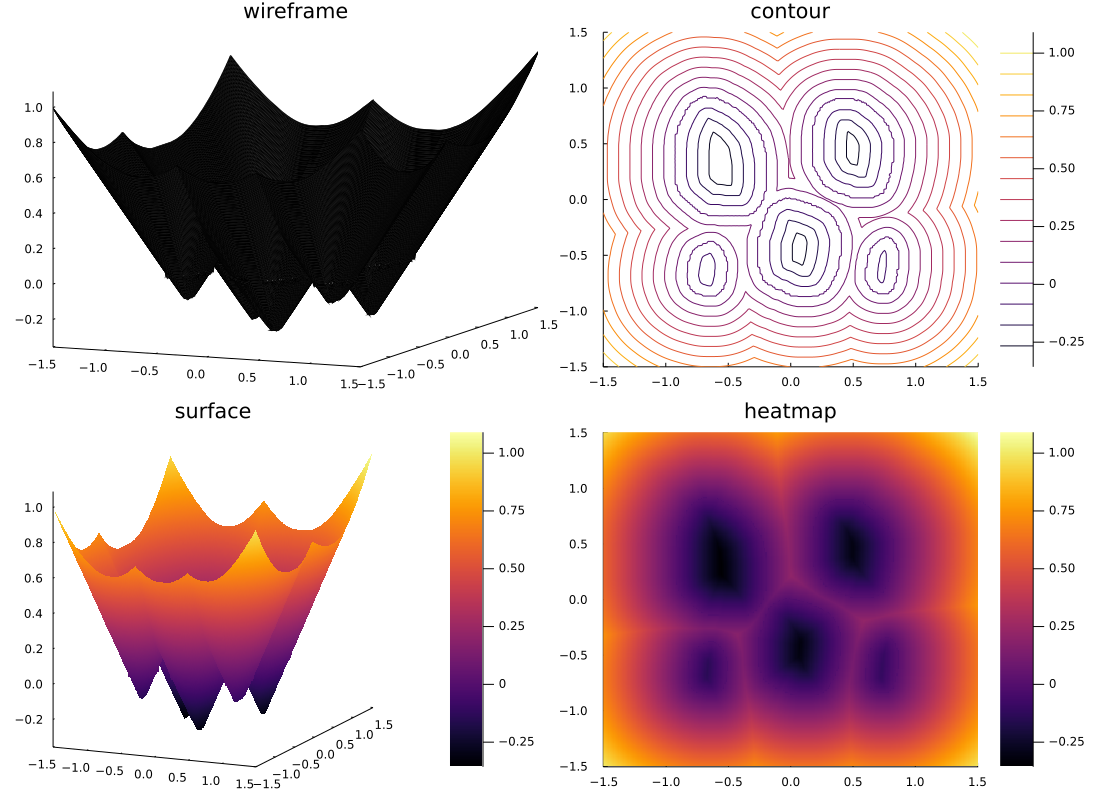
# Development KPT

# Keep

Makefileからshell scriptを呼び出し、簡易的にTDDっぽくしていました。
Demo-for-SignedDistanceFunction.jl (opens new window)にある通り、お絵かきボードを実装し、mock用のデータをすぐに作れるようにしました。
開発の最終段階ではmainブランチをmaster, staging, releaseとし、releaseをdefaultブランチにしました。これによって、リリース版にはMakefileやshell scriptを載せずに済みそうです。

# Problems

Docstringが適当で、method名も適当なところがあります。

# Try

Docstringやmethod名はリファクタリングの必要があります。
公式packageレジストリにリリースをしたいですね。

# Conclusion

課題は残るが、とりあえず使える状態でライブラリをこのように紹介するところまで出来たことは、良いことだと思います。一応構成も一般的なpackageの形をしているし、コメントさえ直せば、公式packageのレジストリにPR送ってもいいんじゃないかな、と考えています。この問題を提供してくれた教授にはとても感謝しているし、議論に参加してくれた学生の仲間にも感謝したいです。この先の予定を全く決めていないので、issueを作っておきます。